Физическая география часть 25

Принцип относительности Галилея устанавли­вает, что законы классической механики во всех ИСО имеют одии и тот же вид. А. Эйнштейн обоб­щил принцип относительности для релятивистской механики: во всех ИСО, движущихся друг относи­тельно друга равномерно и прямолинейно, все за­коны физики имеют один и тот же вид.

Материальная точка — это тело, размерами и формой которого в рассматриваемом случае мож­но пренебречь. Непрерывную линию, описываемую при движении материальной точки относительно выбранной системы отсчета, называют траектори­ей. В зависимости от ее формы движение может быть прямолинейным или криволинейным. При вращательном движении траектории нет.

Тело может двигаться равномерно прямолиней­но или ускоренно. В случае равномерного прямо­линейного движения перемещение определяется по формуле: я — координата вычисляется по фор­муле: х «■ xo + uf, скорость же постоянна: i? «■ const. В случае равноускоренного движения перемещение

а/2

вычисляется по формуле: я «■ Ш + —.

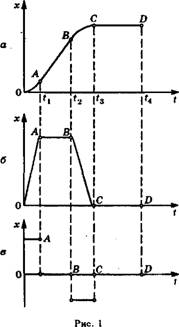
Задача на использование графиков зависимо­стей кинематических величин от времени: Описать характер движения тела, график зависимости ко­ординаты которого от времени изображен на ри­сунке 1, a (OA и ВС — участки парабол). Начер­тить графики скорости и ускорения, соответствую­щие данному движению.

Решение: Соответствующие графики показаны иа рисунке 1, б, в. При их построении учитывается, что в течение промежутка времени от О до t\ тело двигалось равноускоренно, от fi до t-i — равномер­но прямолинейно, от 12 до Рд — равнозамедленно, от до �4 — покоилось.

2. ЗАКОНЫ НЬЮТОНА

Первый закон Ньютона: Существуют системы отсчета, в которых любое изолированное (не под­вергающееся действию внешних сил) тело сохра­няет свое состояние покоя или равномерного пря­молинейного движения. Такие системы отсчета называются инерциальными.

Первый закон Ньютона часто называют законом инерции, поскольку движение, не поддерживаемое никаким воздействием, — это движение по инер­ции. При формулировке закона инерции Ньютон опирался на труды Г. Галилея, который первым по­нял ошибочность утверждения, что тело, на кото­рое ничто не действует, может только покоиться. Галилей показал, что такое тело может либо поко­иться, либо двигаться с постоянной скоростью.

Второй закон Ньютона: Под действием силы F тело массой m приобретет такое ускорение 3, что произведение массы на ускорение будет равно действующей силе, т. е.

тЗ – Р. (1)

Второй закон Ньютона показывает, что причи­ной изменения скорости тела является действие на него окружающих тел.

(2)

В более общей форме второй закон Ньютона за­писывается следующим образом:

Д7 F

где ДД — вызванное действием силы Р изменение импулься тела за время Дt. Формула (1) справед­лива лишь в том случае, когда масса тела т не из­меняется, в то время, как формула (2) верна всегда. Видно, что при т «■ const формула (2) обращается в формулу (1):

Д р Д(‘лР) др

— «= – 7 – та.

&t At Д/

Учитывая принцип суперпозиции сил (равнодей­ствующая нескольких сил равна их векторной сум­ме), второй закон Ньютона можно записать в виде:

тЗ – + … + Рп.

Третий закон Ньютона: При взаимодействии двух тел силы, с которыми они действуют друг на друга, равны по модулю и противоположны по направлению, т. е.

Pl2 » ~Р21 • ‘ (3)

Силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам, но всегда имеют одну природу.

Примерами таких пар сил могут служить: силы гравитационного взаимодействия двух тел; вес тела и сила реакции опоры; кулоновские силы и др.

t

Являясь основой классической механики, зако­ны Ньютона описывают взаимодействия макроско­пических тел, участвующих в не релятивистских движениях (их скорости много меньше скорости света). При этом тела рассматриваются как мате­риальные точки, а движение описывается относи­тельно инерциальных систем отсчета.

Задача на применение второго закона Ньюто­на: Под действием силы F, направленной вдоль го­ризонтальной плоскости, по ее поверхности начи­нает скользить без начальной скорости тело массой т — 4 кг и через t «■ 3 с после начала движения приобретает скорость и — 0,6 м/с. Найти силу F, если коэффициент трения между телом и плоско­стью р «■ 0,2.

Решение: На тело действуют четыре силы: сила Р и сила трения А-р — в горизонтальном направле­нии, сила тяжести Рт и сила реакции опоры N — в вертикальном (рис. 2).

Yn

N

•/S//S/SS/S/SS/)//SS&////f//f//S//S////S//// *

Ft Рис. 2

Направим ось ОХ вдоль направления движения тела, а ось OY — вверх. Запишем уравнение дви­жения тела в проекциях на ось ОХ:

F — Frp ■ ma,

откуда

F – FTp + ma. (1)

Спроецировав вертикально действующие силы на ось OY, получим: N – FT «■ 0 (поскольку про­екция ускорения на ось OY равна нулю). Отсюда, учитывая, что Fr — mg, получаем: N «■ rug. Поэтому сила трения Frp *= pN — pmg. Поскольку тело двигалось равноускоренно без начальной скорости, то его скорость в момент вре­мени t: v «■ at, откуда a — j. Вычислим силу F:

F – pmg + ‘-f – m(ttg + f) «

« 4 кг(о,2 • 9,8 м/с2 + ~ 8,6 Н’

3. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

В 1682 г. И. Ньютон открыл закон всемирного

тяготения: все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональ­ной квадрату расстояния между ними, т. е.

р e Qi’hmt

Коэффициент пропорциональности О называет­

-И Н’М

ся гравитационной постоянной, 0-6,67-10

Взаимное притяжение свойственно всем телам во Вселенной, такое взаимодействие называют гра­витационным.

С помощью закона всемирного тяготения можно описать множество природных явлений: приливы и отливы на Земле, движения естественных и искус­ственных тел как в Солнечной системе, так и за ее пределами и др.

Сила, с которой тела притягиваются к Земле вследствие гравитационного взаимодействия, назы­вается силой тяжести. Согласно закону всемирного тяготения

р_ /-itnM

или Р – rng,

Я2

где g — ускорение свободного падения, R — рассто­яние от центра Земли до тела, М — масса Земли, пг — масса тела.

Движение тела под действием только силы тя­жести называют свободным падением. Свободное падение происходит с ускорением g, которое, как показано выше, не зависит от массы тела. Вблизи – поверхности Земли g = 9,8 м/с2, по мере удаления от Земли эта величина убывает.

Весом тела называют силу, с которой тело дей­ствует на опору или подвес вследствие притяжения к Земле. Вес тела Р, в отличие от силы тяжести, приложен не к данному телу, а к его опоре или под­весу.

В случае свободного падения вес тела равен ну­лю (это состояние невесомости), поскольку само тело и его опора движутся с одинаковым ускорени­ем g. Несмотря на то, что в состоянии невесомости вес тела равен нулю, на него продолжает действо­вать сила тяжести, которая не равна нулю.

4. СИЛА УПРУГОСТИ. ЗАКОН ГУКА

Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещению частиц тела при деформации, назы­вается силой упругости.

Деформацию растяжения или сжатия характе­ризует абсолютное удлинение: Дх = х – *о> где *0 — первоначальная длина образца, ах — его дли­на в деформированном состоянии. Относительным

Д-г

удлинением тела называют отношение е = —.

хо

Закон Гука: Сила упругости, возникающая в теле при его деформации растяжения или сжа­тия, пропорциональна абсолютному удлинению тела: Fynp =

Коэффициент пропорциональности к называет­ся жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геоме­трических размеров и формы.

Отношение модуля силы упругости к площади

поперечного сечения называют механическим на-

F

пряжением: сг — Измеряется механическое

s

напряжение в Паскалях (Па). Использование поня­тия механического напряжения позволяет сформу­лировать закон Гука в более современном виде. Ме­ханическое напряжение, возникающее при дефор­мации тела, пропорционально его относительно­му удлинению, т. е.

сг = Е\е\.

Коэффициент пропорциональности Е называют модулем Юнга (или модулем упругости). Модуль Юнга характеризует сопротивляемость материала упругой деформации. Чем больше модуль Юнга, тем меньше деформируется тело при прочих рав­ных условиях.

Можно установить зависимость жесткости тела k от модуля Юнга Е, а также от длины I и площади поперечного сечения тела S:

„ _ <tS „ _ ES

|Д1| |Д1| |Д1| !0 •

Закон Гука выполняется при небольших дефор­мациях. Предельное напряжение сгп, при котором выполняется ‘закон Гука, называют пределом упру­гости.

5. СИЛА ТРЕНИЯ

Сила, возникающая в месте соприкосновения тел и препятствующая их относительному переме­щению, называется силой трения.

Если тело скользит по какой-либо поверхности, его движению препятствует сила трения сколь­жения, которую можно рассчитать по формуле Frp = fiN, где N — сила реакции опоры, а ц — коэффициент трения скольжения (рис. 3). Коэф­фициент // зависит от материала и качества обра­ботки соприкасающихся поверхностей и не зависит от веса тела.

N

V///////W/WWS.

mg

Рис. 3

Сила трения скольжения всегда направлена про­тивоположно движению тела. При изменении на­правления скорости изменяется и направление си­лы трения.

Сила трения начинает действовать на тело, ко­гда его пытаются сдвинуть с места. Если внешняя сила F меньше произведения fiN, то тело не будет сдвигаться — началу движения, как принято гово­рить, мешает сила трения покоя. Тело начнет дви­жение только тогда, когда внешняя сила F превы­сит максимальное значение, которое может иметь сила трения покоя Ftр.

В некоторых случаях трение полезно (без трения невозможно было бы ходить по земле человеку, жи­вотным, двигаться автомобилям, поездам и т. д.), в таких случаях трение усиливают. Но в других слу­чаях трение вредно. Например, из-за него изнаши­ваются трущиеся детали механизмов, расходуется лишнее горючее на транспорте и т. д. Тогда с тре­нием борются, применяя смазку («жидкостную или воздушную подушку») или заменяя скольжение на качение (поскольку трение качения характеризует­ся значительно меньшими силами, нежели трение скольжения).

6. АРХИМЕДОВА СИЛА

Сила, действующая вертикально вверх на погру­женное в жидкость или газ тело, называется архи­медовой.

Возникновение архимедовой силы объясняется тем, что с увеличением глубины растет давление жидкости (газа). Поэтому силы давления, действу­ющие на нижние элементы поверхности тела, пре­восходят аналогичные силы, действующие на верх­ние элементы поверхности.

Закон Архимеда: На тело, погруженное в жид­кость (газ), действует направленная вертикально вверх выталкивающая сила, равная по величине весу жидкости (газа), взятой в объеме погружен­ного в нее тела (или погруженной части тела):

Fд = gp Ж^т,

где g — ускорение свободного падения, рж — плот­ность жидкости, VT — объем тела, погруженного в жидкость.

В зависимости от соотношения силы тяжести и архимедовой силы, действующих на тело, те­ло будет либо тонуть (�д < FT), либо всплывать (FА > FT), либо находиться в равновесии, т. е. пла­вать (Fa «= FT).

Учитывая формулу для расчета архимедовой си­лы, можно рассмотреть условие плавания тел в за­висимости от соотношения плотностей тела и жид­кости, в которую тело погружено.

Рассматривая случай, когда сила тяжести равна архимедовой, и учитывая, что сила тяжести рав­на FT rng = gpV (m — масса тела, а V и р — его плотность и объем), можно записать равенство двух этих сил gfjжУж = gi>V, откуда 1>ЖУЖ = i>V. Из этого соотношения видно, что при равенстве плот­ностей тела и жидкости тело будет плавать, т. е. остается в равновесии внутри жидкости (посколь­ку Уж «■ V). Если плотность тела меньше плотно­сти жидкости, то часть тела будет выступать над поверхностью (поскольку в этом случае Уж < V). Если же плотность тела больше плотности жидко­сти, то тело будет тонуть (поскольку невозможно, чтобы объем вытесненной жидкости был больше, чем объем тела Vx > V).

7. ИМПУЛЬС ТЕЛА

Векторная физическая величина, равная произ­ведению массы тела на его скорость, называется импульсом тела: р «■ wiT. Под импульсом систе­мы тел понимают сумму импульсов всех тел этой системы: «■ pi + fa + • • • •

Закон сохранении импульса: В замкнутой си­стеме тел при любых процессах ее импульс оста­ется неизменным: рт, = const.

Справедливость этого закона легко доказать, для простоты рассмотрев систему из двух тел. При взаимодействии двух тел изменяется импульс ка­ждого из них, причем эти изменения равны соот­ветственно ДД1 = и = Fz&t. При этом изменение полного импульса системы равно:

Др = Д?1 + Д^2 = Fx Д* + Fz&t – (Fx +

Однако, согласно третьему закону Ньютона,

= – f2- Таким образом, Др = О.

Одним из важнейших следствий закона сохра­нения импульса является существование реактив­ного движения. Реактивное движение возникает в случае, когда от тела с некоторой скоростью отде­ляется какая-либо его часть.

Например, реактивное движение совершает ра­кета. Перед стартом импульс ракеты равен нулю, таким он должен остаться и после старта. При­меняя закон сохранения импульса (действие силы тяжести не учитываем), можно рассчитать, какую скорость разовьет ракета после сгорания в ней всего топлива: mriTr+miT «■ О, где i>r — скорость газов, вы­брасываемых в виде реактивной струи, тГ — масса сгоревшего топлива, v — скорость ракеты, а от — ее масса. Отсюда рассчитываем скорость ракеты:

т

Схемы различных ракет были разработаны К. Э. Циолковским, который считается основопо­ложником теории космических полетов. На прак­тике идеи К. Э. Циолковского стали осуществлять­ся учеными, инженерами и космонавтами под ру­ководством С. П. Королева.

Задача на применение закона сохранения им­пульса: Мальчик массой mi — 50 кг бежит со скоростью i>i — 5 м/с, догоняет тележку массой mi » ЮО кг, движущуюся со скоростью i>2 ~ 2 м/с, и вскакивает иа нее. С какой скоростью v станет двигаться тележка вместе с мальчиком? Треиие не учитывать.

Решение: Систему «мальчик – тележка» мож­но считать изолированной, так как силы тяжести мальчика и тележки уравновешены силами реак­ции опор, а треиие не учитывается.

«1

«2

Yi

I _ I

а <я>

О Yk

ft®

Рис. 4

Свяжем систему отсчета с Землей и направим ось ОХ по направлению движения мальчика и те­лежки (рис. 4, а, б). В этом случае проекции им­пульсов и скоростей иа ось будут равны их моду­лям. Поэтому можно записать соотношения в ска­лярной форме.

Начальный импульс системы складывается из начальных импульсов мальчика и тележки, соот­ветственно равных mivi и Когда мальчик едет иа тележке, импульс системы равен (mi + m2)i>.

По закону сохранения импульса

miPi + m^vz ~ (mi + m%)v. Вычисляем скорость v:

(mit)| + тгиг)

(mi + тг)

3 м/с

(50 кг ■ 5 м/с + 100 кг ■ 2 м/с) (50 кг + 100 кг)

8. МЕХАНИЧЕСКАЯ РАБОТА

•W//J///W////////

7-У//////Л

I я*

Рис. 5

В зависимости от направлений векторов си­лы и перемещения, механическая работа может быть положительной, отрицательной или равной нулю. Например, если вектора Р и 8 совпада­ют, то cos0° — 1, и А > 0. Если векторы F и 8 направлены в противоположные стороны, то cos 180° — -1, и А < 0. Если же Р и 8 перпен­дикулярны, cos 90° — 0, и А — 0.

Мощность характеризует быстроту совершения работы и вычисляется как отношение работы А ко времени t, в течение которого эта работа была со­вершена:

Измеряется мощность в ваттах (Вт). 1 Вт — это мощность, при которой работа в 1 Дж соверша­ется за 1 с: 1 Вт — 1 Дж/с.

Коэффициент полезного действия (КПД) пока­зывает, какую долю составляет полезная работа от всей совершенной (затраченной). КПД равен вы­раженному в процентах отношению полезной рабо­ты ко всей совершенной (затраченной):

„ – dil. Ю0%.

Аа

В силу того что при работе любого механизма приходится преодолевать силы трения, силы со­противления, полезная работа всегда оказывается меньше, чем полная, затраченная: АП < А-,,. По этой причине КПД любого механизма не может быть больше или хотя бы равен 100%.

9. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ

Величину, равную половине произведения мас­сы тела иа квадрат его скорости, называют кинети­ческой энергией:

Е к

mv 2

Физическая величина, равная произведению мо­дуля силы иа модуль перемещения и иа косинус угла между ними, называется механической рабо­той (рис. 5):

А – F • a • cos ip.

Работа — величина скалярная. Измеряется ра­бота в джоулях (Дж). 1 Дж — это работа, совер­шенная силой 1 Н иа перемещении 1 м.

Изменение кинетической энергии тела за некото­рый промежуток времени равно работе, совершен­ной за это время силой, действующей на тело:

А – Д�к.

Оср

Если работа силы по любой замкнутой траек­тории равна нулю, силу называют потенциальной. Работа потенциальных сил не зависит от траекто­рии, а определяется только начальным и конечным положением тела. Величину, равную работе, кото­рую должна совершить потенциальная сила, чтобы переместить тело из рассматриваемого положения в нулевое, называют потенциальной энергией тела. В нулевом положении потенциальная энергия тела считается равной нулю.

(2)

Для разных видов сил существуют разные фор­мулы потенциальной энергии. Например, для тела, взаимодействующего с Землей и находящегося на высоте h над ее поверхностью,

Е п – mgh

= 32000 Н – 32 кН;

10″

2,5- Ю-4 с.

(нулевое положение — поверхность Земли), а для тела, на которое действует пружина жесткости k, растянутая на величину х,

Еп

кх» 2

Время движения пули в дереве равно: t — —,

ие р

где иСр — средняя скорость. В силу того что дви­жение равнозамедленное, средняя скорость равна полусумме начальной и конечной скоростей:

0

2

следовательно,

t-

v

Вычисляем силу F и время t:

10 • 10″а кг • (800 м/с) 2-10- 10~2 м

t – 2 ‘ 10

800 м/с

(нулевое положение — точка, где х = О).

Работа потенциальных сил равна изменению по­тенциальной энергии, взятому с противоположным знаком: А — – ДЕп.

Сумму кинетической и потенциальной энергий тела называют его полной механической энергией. Бели система тел консервативна (т. е. на нее дей­ствуют лишь не зависящие от времени потенциаль­ные силы), то для нее справедлив закон сохранения механической энергии: При любых процессах, про­исходящих в системе тел, ее полная механическая энергия остается неизменной, т. е. Е — const. В этом случае при всяком увеличении кинетической энергии потенциальная энергия уменьшается ровно на столько же, и наоборот.

Задача на Применение закона сохранения ме­ханической энергия: Пуля массой т — 10 г, летя­щая со скоростью v = 800 м/с, попадает в дерево и углубляется на 8 = 10 см. Найти среднюю силу F сопротивления дерева и время t движения пули в дереве, считая это движение равнозамедленным (рис. 6).

Рис. в,

Решение: Подлетая к дереву, пуля обладала ки-

2

нетической энергией Ек = ——, которая полностью пошла на преодоление сил сопротивления дерева:

— Fs,

откуда

10. гармонические колебания

Движения, которые точно повторяются через равные интервалы времени, называются гармони­ческими колебаниями. Эти колебания происходят по закону синуса или косинуса.

Уравнение гармонических колебаний имеет вид:

q – qm • sin(wt + <p0).

где qm — амплитуда колебаний (наибольшее рас­стояние, на которое тело удаляется от положения равновесия), w — циклическая частота колеба­ний (число колебаний, совершаемых за 27Г секунд), од — начальная фаза колебаний.

Частота колебаний е/ — количество колебаний за секунду. Если за время t совершено п колебаний, то

Частота связана с циклической частотой соотноше­нием:

w – 2т/.

Время, за которое происходит одно полное коле­бание, называется периодом колебаний Т. Период определяется по формуле

Т —

п >

Сравнивая формулы для расчета частоты и периода, можно заметить, что это обратные величины:

Г-1.

V

Величина, стоящая под знаком синуса или ко­синуса в уравнении гармонических колебаний, на­зывается фазой колебаний:

Фаза является той величиной, которая при за­данной амплитуде определяет координату.